Sound Field Synthesis Toolbox for Python¶
Python implementation of the Sound Field Synthesis Toolbox.
- Documentation:
- http://sfs.rtfd.org/
- Code:
- http://github.com/sfstoolbox/sfs-python/
- Python Package Index:
- http://pypi.python.org/pypi/sfs/
Requirements¶
Obviously, you’ll need Python. We normally use Python 3.x, but it should also work with Python 2.x. NumPy and SciPy are needed for the calcuations. If you also want to plot the resulting sound fields, you’ll need matplotlib.
Instead of installing all of them separately, you should probably get a Python distribution that already includes everything, e.g. Anaconda.
Installation¶
Once you have installed the above-mentioned dependencies, you can use pip to download and install the latest release with a single command:
pip install sfs --user
If you want to install it system-wide for all users (assuming you have the
necessary rights), you can just drop the --user option.
To un-install, use:
pip uninstall sfs
If you want to keep up with the latest and greatest development version you should get it from Github:
git clone https://github.com/sfstoolbox/sfs-python.git
cd sfs-python
python setup.py develop --user
How to Get Started¶
Various examples are located in the directory examples/
- sound_field_synthesis.py:
Illustrates the general usage of the toolbox
- horizontal_plane_arrays.py:
Computes the sound fields for various techniques, virtual sources and loudspeaker array configurations
- soundfigures.py:
Illustrates the synthesis of sound figures with Wave Field Synthesis
API Documentation¶
Loudspeaker Arrays¶
Compute positions of various secondary source distributions.
import sfs
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 8, 4 # inch
plt.rcParams['axes.grid'] = True
-
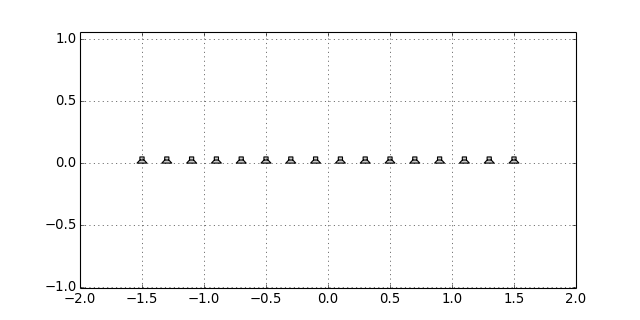
sfs.array.linear(N, spacing, center=[0, 0, 0], n0=[1, 0, 0])[source]¶ Linear secondary source distribution.
Parameters: - N (int) – Number of loudspeakers.
- spacing (float) – Distance (in metres) between loudspeakers.
- center ((3,) array_like, optional) – Coordinates of array center.
- n0 ((3,) array_like, optional) – Normal vector of array.
Returns: - positions ((N, 3) numpy.ndarray) – Positions of secondary sources
- directions ((N, 3) numpy.ndarray) – Orientations (normal vectors) of secondary sources
- weights ((N,) numpy.ndarray) – Weights of secondary sources
Example
x0, n0, a0 = sfs.array.linear(16, 0.2, n0=[0, -1, 0]) sfs.plot.loudspeaker_2d(x0, n0, a0) plt.axis('equal')
-
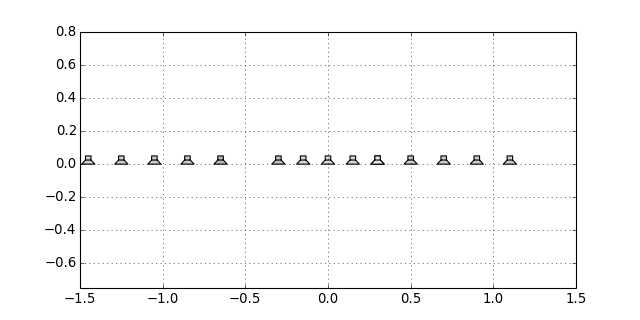
sfs.array.linear_nested(N, dx1, dx2, center=[0, 0, 0], n0=[1, 0, 0])[source]¶ Nested linear secondary source distribution.
Example
x0, n0, a0 = sfs.array.linear_nested(16, 0.15, 0.2, n0=[0, -1, 0]) sfs.plot.loudspeaker_2d(x0, n0, a0) plt.axis('equal')
-
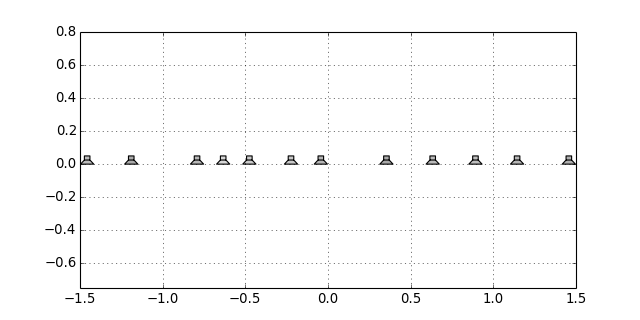
sfs.array.linear_random(N, dy1, dy2, center=[0, 0, 0], n0=[1, 0, 0])[source]¶ Randomly sampled linear array.
Example
x0, n0, a0 = sfs.array.linear_random(12, 0.15, 0.4, n0=[0, -1, 0]) sfs.plot.loudspeaker_2d(x0, n0, a0) plt.axis('equal')
-
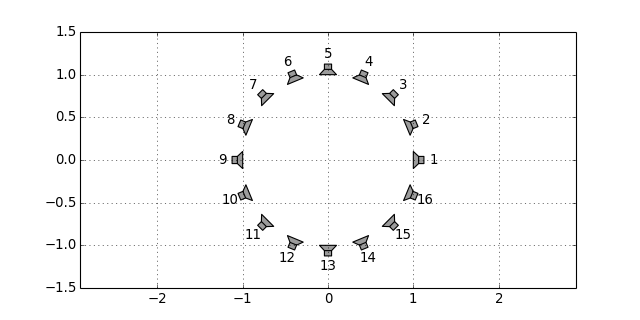
sfs.array.circular(N, R, center=[0, 0, 0])[source]¶ Circular secondary source distribution parallel to the xy-plane.
Example
x0, n0, a0 = sfs.array.circular(16, 1) sfs.plot.loudspeaker_2d(x0, n0, a0, size=0.2, show_numbers=True) plt.axis('equal')
-
sfs.array.rectangular(Nx, dx, Ny, dy, center=[0, 0, 0], n0=None)[source]¶ Rectangular secondary source distribution.
Example
x0, n0, a0 = sfs.array.rectangular(8, 0.2, 4, 0.2) sfs.plot.loudspeaker_2d(x0, n0, a0, show_numbers=True) plt.axis('equal')
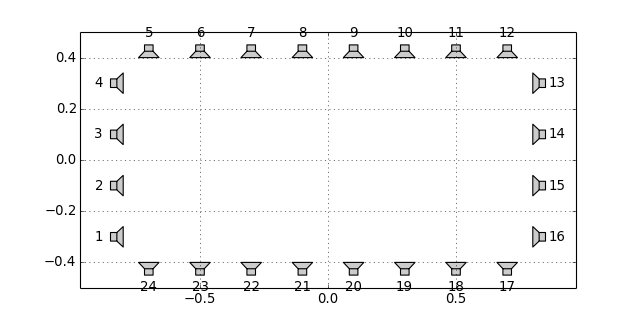
-
sfs.array.rounded_edge(Nxy, Nr, dx, center=[0, 0, 0], n0=None)[source]¶ Array along the xy-axis with rounded edge at the origin.
Parameters: - Nxy (int) – Number of secondary sources along x- and y-axis.
- Nr (int) – Number of secondary sources in rounded edge. Radius of edge is adjusted to equdistant sampling along entire array.
- center ((3,) array_like, optional) – Position of edge.
- n0 ((3,) array_like, optional) – Normal vector of array. Default orientation is along xy-axis.
Returns: - positions ((N, 3) numpy.ndarray) – Positions of secondary sources
- directions ((N, 3) numpy.ndarray) – Orientations (normal vectors) of secondary sources
- weights ((N,) numpy.ndarray) – Integration weights of secondary sources
Example
x0, n0, a0 = sfs.array.rounded_edge(8, 5, 0.2) sfs.plot.loudspeaker_2d(x0, n0, a0) plt.axis('equal')
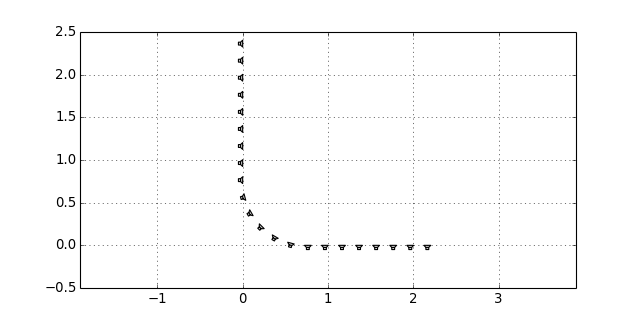
-
sfs.array.planar(Ny, dy, Nz, dz, center=[0, 0, 0], n0=None)[source]¶ Planar secondary source distribtion.
-
sfs.array.cube(Nx, dx, Ny, dy, Nz, dz, center=[0, 0, 0], n0=None)[source]¶ Cube shaped secondary source distribtion.
-
sfs.array.sphere_load(fname, radius, center=[0, 0, 0])[source]¶ Spherical secondary source distribution loaded from datafile.
ASCII Format (see MATLAB SFS Toolbox) with 4 numbers (3 position, 1 weight) per secondary source located on the unit circle.
-
sfs.array.load(fname, center=[0, 0, 0], n0=None)[source]¶ Load secondary source positions from datafile.
Comma Seperated Values (CSV) format with 7 values (3 positions, 3 directions, 1 weight) per secondary source.
Tapering¶
Weights (tapering) for the driving function.
Monochromatic Sources¶
Compute the sound field generated by a sound source.
import sfs
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 8, 4 # inch
x0 = 1.5, 1, 0
f = 500 # Hz
omega = 2 * np.pi * f
grid = sfs.util.xyz_grid([-2, 3], [-1, 2], 0, spacing=0.02)
-
sfs.mono.source.point(omega, x0, n0, grid, c=None)[source]¶ Point source.
1 e^(-j w/c |x-x0|) G(x-x0, w) = --- ----------------- 4pi |x-x0|Examples
p_point = sfs.mono.source.point(omega, x0, None, grid) sfs.plot.soundfield(p_point, grid) plt.title("Point Source at {} m".format(x0))
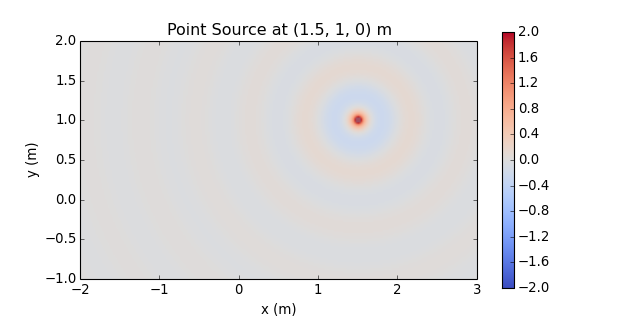
Normalization ... multiply by \(4\pi\) ...
p_point *= 4 * np.pi sfs.plot.soundfield(p_point, grid) plt.title("Point Source at {} m (normalized)".format(x0))
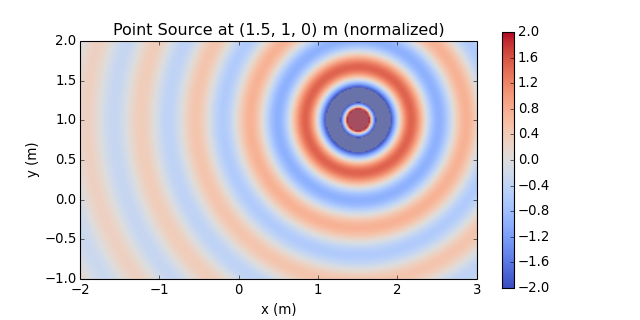
-
sfs.mono.source.point_modal(omega, x0, n0, grid, L, N=None, deltan=0, c=None)[source]¶ Point source in a rectangular room using a modal room model.
Parameters: - omega (float) – Frequency of source.
- x0 ((3,) array_like) – Position of source.
- n0 ((3,) array_like) – Normal vector (direction) of source (only required for compatibility).
- grid (triple of numpy.ndarray) – The grid that is used for the sound field calculations.
- L ((3,) array_like) – Dimensionons of the rectangular room.
- N ((3,) array_like or int, optional) – Combination of modal orders in the three-spatial dimensions to calculate the sound field for or maximum order for all dimensions. If not given, the maximum modal order is approximately determined and the sound field is computed up to this maximum order.
- deltan (float, optional) – Absorption coefficient of the walls.
- c (float, optional) – Speed of sound.
Returns: numpy.ndarray – Sound pressure at positions given by grid.
-
sfs.mono.source.line(omega, x0, n0, grid, c=None)[source]¶ Line source parallel to the z-axis.
Note: third component of x0 is ignored.
(2) G(x-x0, w) = -j/4 H0 (w/c |x-x0|)
Examples
p_line = sfs.mono.source.line(omega, x0, None, grid) sfs.plot.soundfield(p_line, grid) plt.title("Line Source at {} m".format(x0[:2]))
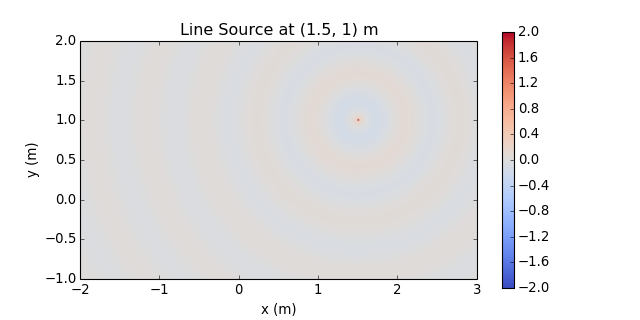
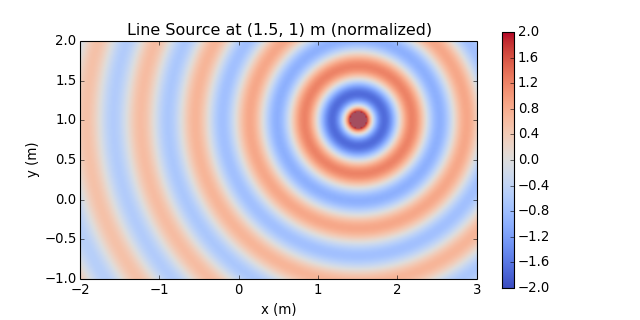
Normalization ...
p_line *= np.exp(-1j*7*np.pi/4) / np.sqrt(1/(8*np.pi*omega/sfs.defs.c)) sfs.plot.soundfield(p_line, grid) plt.title("Line Source at {} m (normalized)".format(x0[:2]))
-
sfs.mono.source.line_dipole(omega, x0, n0, grid, c=None)[source]¶ Line source with dipole characteristics parallel to the z-axis.
Note: third component of x0 is ignored.
(2) G(x-x0, w) = jk/4 H1 (w/c |x-x0|) cos(phi)
-
sfs.mono.source.plane(omega, x0, n0, grid, c=None)[source]¶ Plane wave.
G(x, w) = e^(-i w/c n x)
Example
direction = 45 # degree n0 = sfs.util.direction_vector(np.radians(direction)) p_plane = sfs.mono.source.plane(omega, x0, n0, grid) sfs.plot.soundfield(p_plane, grid); plt.title("Plane wave with direction {} degree".format(direction))
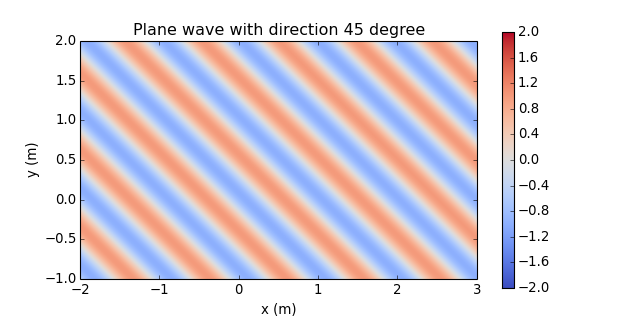
Monochromatic Driving Functions¶
Compute driving functions for various systems.
-
sfs.mono.drivingfunction.wfs_2d_line(omega, x0, n0, xs, c=None)[source]¶ Line source by 2-dimensional WFS.
D(x0,k) = j k (x0-xs) n0 / |x0-xs| * H1(k |x0-xs|)
-
sfs.mono.drivingfunction.wfs_2d_point(omega, x0, n0, xs, c=None)¶ Point source by two- or three-dimensional WFS.
(x0-xs) n0 D(x0,k) = j k ------------- e^(-j k |x0-xs|) |x0-xs|^(3/2)
-
sfs.mono.drivingfunction.wfs_25d_point(omega, x0, n0, xs, xref=[0, 0, 0], c=None, omalias=None)[source]¶ Point source by 2.5-dimensional WFS.
____________ (x0-xs) n0 D(x0,k) = \|j k |xref-x0| ------------- e^(-j k |x0-xs|) |x0-xs|^(3/2)
-
sfs.mono.drivingfunction.wfs_3d_point(omega, x0, n0, xs, c=None)¶ Point source by two- or three-dimensional WFS.
(x0-xs) n0 D(x0,k) = j k ------------- e^(-j k |x0-xs|) |x0-xs|^(3/2)
-
sfs.mono.drivingfunction.wfs_2d_plane(omega, x0, n0, n=[0, 1, 0], c=None)¶ Plane wave by two- or three-dimensional WFS.
Eq.(17) from [Spors et al, 2008]:
D(x0,k) = j k n n0 e^(-j k n x0)
-
sfs.mono.drivingfunction.wfs_25d_plane(omega, x0, n0, n=[0, 1, 0], xref=[0, 0, 0], c=None, omalias=None)[source]¶ Plane wave by 2.5-dimensional WFS.
____________ D_2.5D(x0,w) = \|j k |xref-x0| n n0 e^(-j k n x0)
-
sfs.mono.drivingfunction.wfs_3d_plane(omega, x0, n0, n=[0, 1, 0], c=None)¶ Plane wave by two- or three-dimensional WFS.
Eq.(17) from [Spors et al, 2008]:
D(x0,k) = j k n n0 e^(-j k n x0)
-
sfs.mono.drivingfunction.delay_3d_plane(omega, x0, n0, n=[0, 1, 0], c=None)[source]¶ Plane wave by simple delay of secondary sources.
-
sfs.mono.drivingfunction.source_selection_plane(n0, n)[source]¶ Secondary source selection for a plane wave.
Eq.(13) from [Spors et al, 2008]
-
sfs.mono.drivingfunction.source_selection_point(n0, x0, xs)[source]¶ Secondary source selection for a point source.
Eq.(15) from [Spors et al, 2008]
-
sfs.mono.drivingfunction.nfchoa_2d_plane(omega, x0, r0, n=[0, 1, 0], c=None)[source]¶ Point source by 2.5-dimensional WFS.
-
sfs.mono.drivingfunction.nfchoa_25d_point(omega, x0, r0, xs, c=None)[source]¶ Point source by 2.5-dimensional WFS.
__ (2) 1 \ h|m| (w/c r) D(phi0,w) = ----- /__ ------------- e^(i m (phi0-phi)) 2pi r0 m=-N..N (2) h|m| (w/c r0)
-
sfs.mono.drivingfunction.nfchoa_25d_plane(omega, x0, r0, n=[0, 1, 0], c=None)[source]¶ Plane wave by 2.5-dimensional WFS.
__ 2i \ i^|m| D_25D(phi0,w) = -- /__ ------------------ e^(i m (phi0-phi_pw) ) r0 m=-N..N (2) w/c h|m| (w/c r0)
-
sfs.mono.drivingfunction.sdm_2d_line(omega, x0, n0, xs, c=None)[source]¶ Line source by two-dimensional SDM.
The secondary sources have to be located on the x-axis (y0=0). Derived from [Spors 2009, 126th AES Convention], Eq.(9), Eq.(4):
D(x0,k) =
-
sfs.mono.drivingfunction.sdm_2d_plane(omega, x0, n0, n=[0, 1, 0], c=None)[source]¶ Plane wave by two-dimensional SDM.
The secondary sources have to be located on the x-axis (y0=0). Derived from [Ahrens 2011, Springer], Eq.(3.73), Eq.(C.5), Eq.(C.11):
D(x0,k) = kpw,y * e^(-j*kpw,x*x)
Monochromatic Sound Fields¶
Computation of synthesized sound fields.
Plotting¶
Plot sound fields etc.
-
sfs.plot.virtualsource_2d(xs, ns=None, type='point', ax=None)[source]¶ Draw position/orientation of virtual source.
-
sfs.plot.loudspeaker_2d(x0, n0, a0=0.5, size=0.08, show_numbers=False, grid=None, ax=None)[source]¶ Draw loudspeaker symbols at given locations and angles.
Parameters: - x0 ((N, 3) array_like) – Loudspeaker positions.
- n0 ((N, 3) or (3,) array_like) – Normal vector(s) of loudspeakers.
- a0 (float or (N,) array_like, optional) – Weighting factor(s) of loudspeakers.
- size (float, optional) – Size of loudspeakers in metres.
- show_numbers (bool, optional) – If
True, loudspeaker numbers are shown. - grid (triple of numpy.ndarray, optional) – If specified, only loudspeakers within the grid are shown.
- ax (Axes object, optional) – The loudspeakers are plotted into this
Axesobject or – if not specified – into the current axes.
-
sfs.plot.loudspeaker_3d(x0, n0, a0=None, w=0.08, h=0.08)[source]¶ Plot positions and normals of a 3D secondary source distribution.
Utilities¶
Various utility functions.
-
sfs.util.direction_vector(alpha, beta=1.5707963267948966)[source]¶ Compute normal vector from azimuth, colatitude.
-
sfs.util.asarray_1d(a, **kwargs)[source]¶ Squeeze the input and check if the result is one-dimensional.
Returns a converted to a
numpy.ndarrayand stripped of all singleton dimensions. Scalars are “upgraded” to 1D arrays. The result must have exactly one dimension. If not, an error is raised.
-
sfs.util.asarray_of_rows(a, **kwargs)[source]¶ Convert to 2D array, turn column vector into row vector.
Returns a converted to a
numpy.ndarrayand stripped of all singleton dimensions. If the result has exactly one dimension, it is re-shaped into a 2D row vector.
-
sfs.util.asarray_of_arrays(a, **kwargs)[source]¶ Convert the input to an array consisting of arrays.
A one-dimensional
numpy.ndarraywith dtype=object is returned, containing the elements of a asnumpy.ndarray(whose dtype and other options can be specified with **kwargs).
-
sfs.util.strict_arange(start, stop, step=1, endpoint=False, dtype=None, **kwargs)[source]¶ Like
numpy.arange(), but compensating numeric errors.Unlike
numpy.arange(), but similar tonumpy.linspace(), providing endpoint=True includes both endpoints.Parameters: start, stop, step, dtype – See
numpy.arange().endpoint – See
numpy.linspace().Note
With endpoint=True, the difference between start and end value must be an integer multiple of the corresponding spacing value!
**kwargs – All further arguments are forwarded to
numpy.isclose().
Returns: numpy.ndarray – Array of evenly spaced values. See
numpy.arange().
-
sfs.util.xyz_grid(x, y, z, spacing, endpoint=True, **kwargs)[source]¶ Create a grid with given range and spacing.
Parameters: - x, y, z (float or pair of float) – Inclusive range of the respective coordinate or a single value if only a slice along this dimension is needed.
- spacing (float or triple of float) – Grid spacing. If a single value is specified, it is used for all dimensions, if multiple values are given, one value is used per dimension. If a dimension (x, y or z) has only a single value, the corresponding spacing is ignored.
- endpoint (bool, optional) – If
True(the default), the endpoint of each range is included in the grid. UseFalseto get a result similar tonumpy.arange(). Seestrict_arange(). - **kwargs – All further arguments are forwarded to
strict_arange().
Returns: list of numpy.ndarrays – A grid that can be used for sound field calculations.
See also